Đây là nội dung bài talk của mình trong buổi meetup Trà đá 2^2, 25/08/2018, slide.
Xem phần trước tại đây.
Trang 14: Cuối cùng thì một Deep Neural Networks (DNN) là gì?
Về mặt bản chất toán học thì các (Feed-forward) DNN nói chung thực ra rất “đơn giản”: Chúng là hàm hợp của một số các hàm “cơ bản” khác, như hàm identity $ f(x) = x $, hàm linear $ f(x) = ax + b $, hàm ReLU $ f(x) = max(x, 0) $, hoặc phức tạp một chút như hàm $ tanh(x) $, hay hàm sigmoid $ f(x) = \frac{e^x}{1 + e^x} $. Tuy từng hàm, từng “neuron”, từng layer là “đơn giản”, nhưng khi kết hợp lại với nhau thì lại rất “hữu hiệu”, chính là do định lý dưới đây:
Định lý xấp xỉ phổ quát (Universal Approximation Theorem): Bất kỳ một hàm số thực liên tục trên tập compact, đều có thể được xấp xỉ bằng một Feed-forward DNN một lớp với hữu hạn số “neuron”, nếu “hàm kích hoạt”, activation function, đảm bảo được các điều kiện sau trên tập xác định: (1) bị chặn, (2) liên tục, (3) đơn điệu tăng.
Ý nghĩa của định lý này là: Với một hàm liên tục trên tập compact cho trước, sẽ tồn tại một DNN với chỉ một lớp, có thể xấp xỉ được hàm này, bất kể hàm cho trước đó phức tạp như thế nào. Nên nhớ rằng đây chỉ là existence/non-constructive theorem, nghĩa là ta biết được rằng nó tồn tại, nhưng định lý không chỉ ra cách xây dựng nó như thế nào. Một số kết quả cải tiến hơn cũng chứng minh được rằng: Với mọi hàm số thực $ n $ chiều liên tục trên tập compact, luôn tồn tại một DNN có một lớp, với $ n + 3 $ ReLU “neuron”, có thể xấp xỉ được hàm đã cho.
Tất cả chỉ là.. lý thuyết. Việc tồn tại một DNN như thế không đảm bảo rằng ta có thể train được một DNN có thể “hội tụ” về DNN tối ưu đó. Các kết quả thực nghiệm khuyến khích việc sử dụng các network nhiều lớp, thậm chí số lớp có thể lên đến hàng ngàn. “Stack more layers” vì thế cũng trở thành meme trong ngành.
Trang 15: Tóm lại thì DNN, mà nói rộng ra hơn là Deep learning, là một công cụ rất mạnh và hữu hiệu để xấp xỉ những hàm số phức tạp. Hàm số ở đây nói theo nghĩa phổ quát, như:
Dữ liệu đầu vào là hình ảnh và đầu ra là 1 hoặc 0, lần lượt chỉ việc trong ảnh có con chó hay con mèo, là một hàm số.
Dữ liệu đầu vào là lịch sử mua sắm của tất cả người dùng trên một platform, đầu ra là món hàng mà người dùng X bất kỳ muốn mua, là một hàm số.
Trong ngôn ngữ Machine learning thì hàm số đồng nghĩa với mô hình. Và Deep learning là một công cụ rất mạnh để tạo ra các mô hình. Một câu hỏi tự nhiên được đặt ra là: Nếu Deep learning mạnh như vậy, thì còn chờ gì mà không áp dụng nó vào mọi mô hình?
Song đề Bias-Variance (Bias-Variance tradeoff): Hai “nguồn” sai số, error, của một mô hình đến từ bias của mô hình, tức mô hình quá đơn giản và đưa ra quá nhiều giả định về dữ liệu, dẫn đến “underfitting”, hoặc variance, tức mô hình quá phức tạp, nên nhạy cảm với những sự thay đổi nhỏ từ dữ liệu, vốn luôn có nhiễu, dẫn đến “overfitting”.
Deep learning thuộc lớp mô hình có variance cao, do hàm số mà một mô hình Deep learning học được có thể rất phức tạp. Trong Machine learning cổ điển, hiện tượng “overfitting” thường đến từ việc người sử dụng không hiểu hết mô hình của mình, với một số lỗi căn bản thường gặp của các “tay mơ” khi training như:
Sử dụng đa thức bậc cao, gần
$ n $, để xấp xỉ hàm số cho$ n $điểm trong không gian 2 chiềuDùng mô hình k-nearest neighbor (kNN) với
$ k = 0, 1 $
Các lỗi này thuộc dạng rất “silly” của những người mới bắt đầu học. Do phần lớn các mô hình Machine learning cổ điển thường yêu cầu một sự hiểu biết nhất định vào dữ liệu mà mình có, nên việc “overfitting” trong Machine learning cổ điển nhìn chung thường “ít” hơn trong Deep learning.
Trong Deep learning thì “overfitting” là hiện tượng chung, là thứ gần như không thể tránh khỏi khi làm việc với Feed-forward DNN cũng như các dạng nâng cao khác của nó như Convolutional Neural Network (CNN) hay Recurrent Neural Network (RNN). Việc có “overfitting” trong mô hình Deep learning không đến từ sự thiếu hiểu biết của người làm mô hình, mà gần như thuộc về bản chất của mô hình.
Update 09/2019: Mới đây có môt bài báo rất thú vị, nội dung là xét lại Song đề Bias-Variance. Thực nghiệm trong Deep learning cho thấy các mô hình có nhiều lớp, thậm chí cả ngàn lớp, thường cho kết quả tốt hơn các mô hình “shallow”:
Theo lý thuyết cổ điển, việc tăng độ phức tạp của mô hình sẽ chỉ giúp mô hình cải thiện lúc “ban đầu”: Nghĩa là sẽ tồn tại một thời điểm, tạm gọi là “cut-off point”, mà khi đó, nếu nâng độ phức tạp hiện tại của mô hình, thì mô hình sẽ không cải thiện được nữa, thậm chí còn cho kết quả tệ hơn (classic U-shaped test error curve).
Bài báo này đã cho thấy, bằng thực nghiệm, rằng đây chỉ là một phần của vấn đề: Nếu tiếp tục tăng độ phức tạp lên mãi, thì sau một thời gian, mô hình sẽ lại tiếp tục cải thiện, và sẽ cho kết quả tốt hơn tại điểm “cut-off point” được nói ở trên.

Ảnh được lấy từ bài báo Reconciling modern machine learning practice and the bias-variance trade-off.
Machine learning cổ điển tập trung vào việc tìm ra cái “cut-off point” kia, để có được một mô hình cân bằng giữa Bias và Variance. Deep learning hiện tại tập trung vào việc tăng độ phức tạp của mô hình, với niềm tin là sẽ có một mô hình tốt hơn, và điều này đã được kiểm chứng bằng thực nghiệm.
Song đề Bias-Variance hay được so sánh với Dao cạo Occam (Occam’s razor): Với nhiều cách lý giải sự việc, hãy chọn cách lý giải đơn giản nhất. Phiên bản “mới” của Dao cạo Occam, sau phát hiện này, hẳn sẽ có dạng: Với các vấn đề đơn giản, hãy lý giải một cách đơn giản; Nhưng với các vấn đề phức tạp, đừng “ngại” lý giải nó một cách “phức tạp hơn”. Keep it simple, but not simpler!
Trang 16 - 17: Ví dụ kinh điển dưới đây của Ian Goodfellow và các đồng nghiệp đã cho thấy sự “nghiêm trọng” của vấn đề “overfitting” trong “mạng neuron” như thế nào:

Ảnh được lấy từ bài báo Explaining and Harnessing Adversarial Examples.
Bức ảnh con gấu trúc ban đầu được nhận dạng chính xác bởi mô hình GoogLeNet, một trong những mô hình “nhận dạng vật thể”, object detection, thuộc dạng “State-of-the-art” (SOTA), tức là tốt nhất ở thời điểm đó. Khi thêm một lớp “nhiễu” ngẫu nhiên vào hình gốc, mặc dù hình kết quả không thay đổi về ý nghĩa, và với người thường thì về mặt thị giác là rất khó phân biệt, nhưng mô hình trên lại đưa ra dự đoán sai lầm là “gibbon” với xác suất trả về là 99.3%, so với dự đoán “panda” 57.7% cho hình gốc.
Gần đây hơn, một bài báo khác đã đưa ra một phương pháp mới, còn “cực đoan” hơn so với cách tiếp cận ban đầu của Goodfellow: Phương pháp mới này chỉ cần sửa duy nhất 1 pixel là đã đủ để các mô hình SOTA không chỉ đưa ra dự đoán sai, mà còn đưa ra dự đoán sai với “độ tin cậy” cao!

Ảnh được lấy từ bài báo One pixel attack for fooling deep neural networks.
Ngoài lề: Cũng từ những nghiên cứu về “Adversarial Examples”, Ian Goodfellow đã trở thành một trong số những người tiên phong, mở ra một hướng nghiên cứu mới trong Machine learning hiện đại, đó chính là Generative Adversarial Network.
Trang 18: Ảnh và ý tưởng cho phần này được lấy từ bài viết Neural Networks, Manifolds, and Topology của Christopher Colah.
Để hiểu được vì sao Deep learning dễ “overfitting” như vậy, ta phải hiểu được việc huấn luyện một “mạng neuron” diễn ra như thế nào. Dưới đây là hai ví dụ đơn giản, giúp ta nhìn thấy (một phần) trong bức tranh tổng thể của việc huấn luyện một “mạng neuron”.
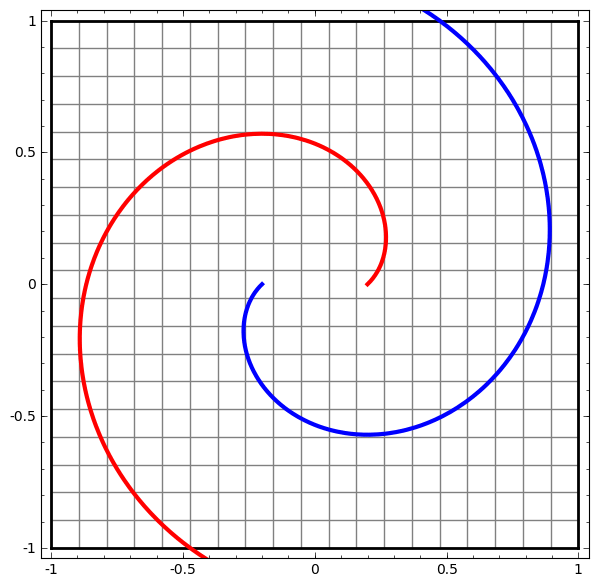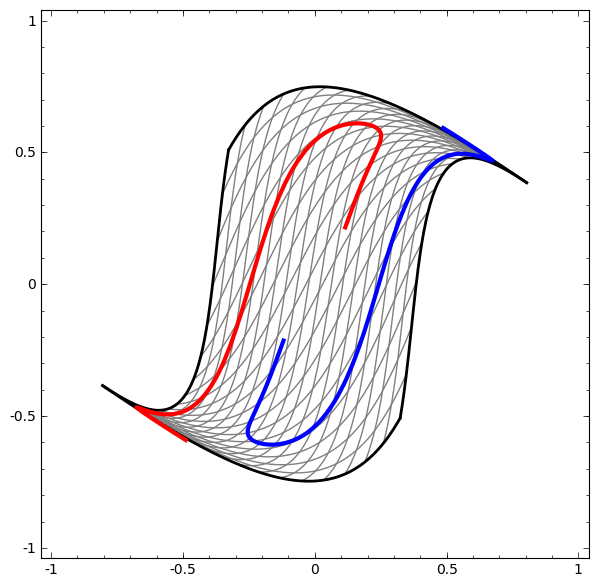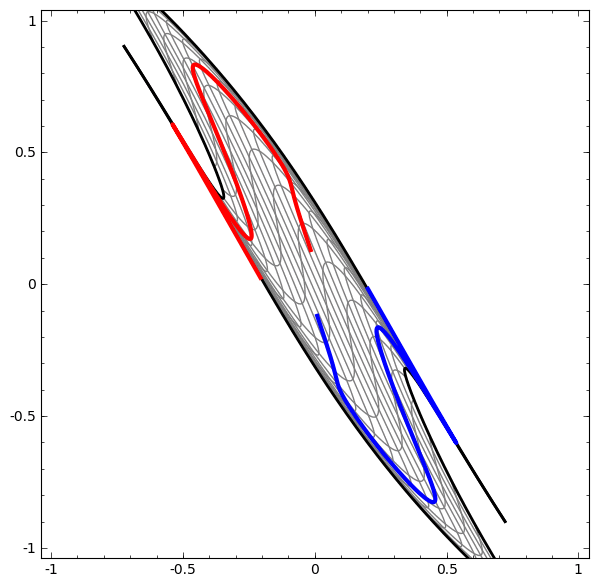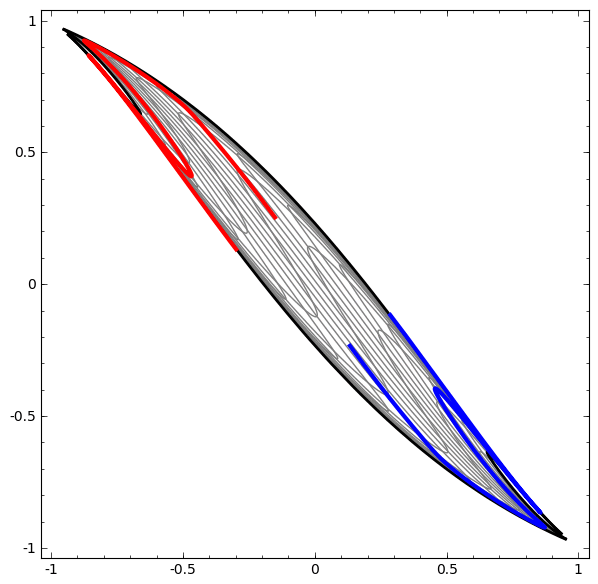
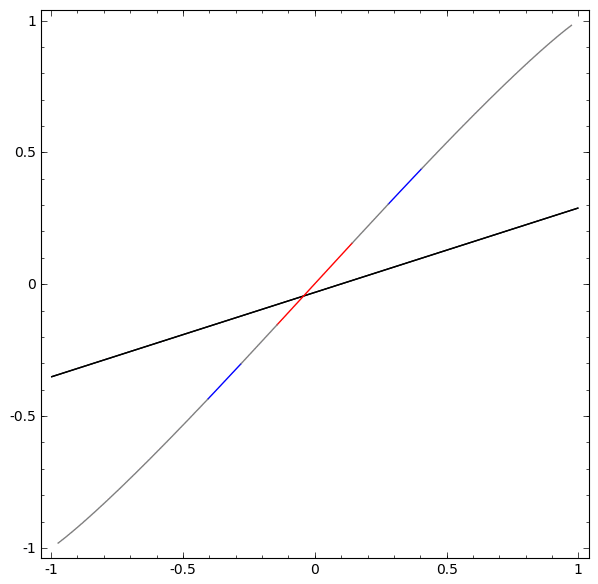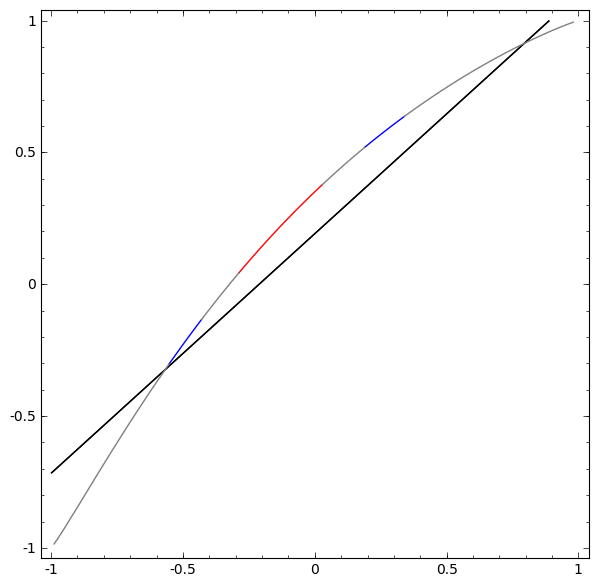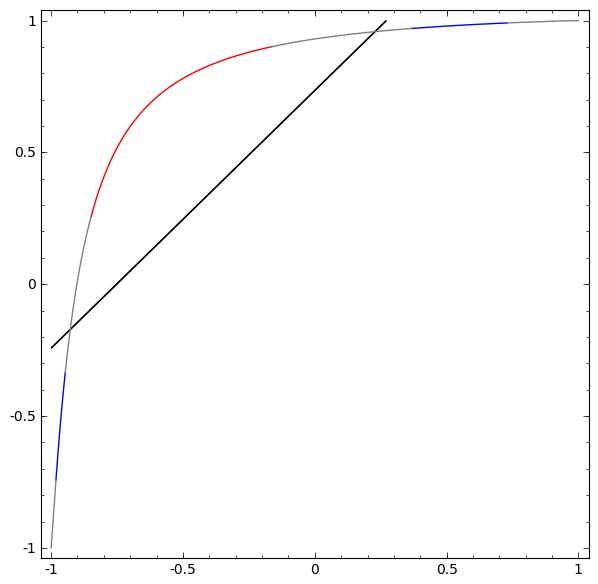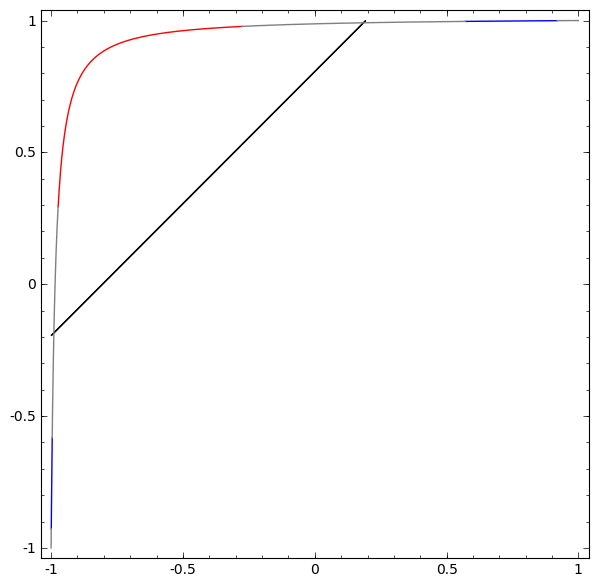
Một cách “vĩ mô”, điểm mấu chốt trong quá trình huấn luyện là: Các phương pháp tối ưu sẽ cố gắng tìm một “đa tạp”, manifold, mà nói rộng ra hơn là học một “biểu diễn”, representation, sao cho “biểu diễn” học được ở lớp mới có thể giúp mô hình dễ dàng đưa ra dự đoán nhất. Như trong hai ví dụ trên, do lớp cuối cùng trong mô hình là một lớp có dạng “logistic regression”, mô hình sẽ “cố gắng” làm cho hai tập được “tách biệt tuyến tính”, linear separable, nghĩa là làm cho hai tập dễ được tách biệt bằng một siêu phẳng trong không gian đa chiều.
Bài viết của Colah cho ta thêm nhiều insights hơn về câu hỏi “Vì sao điều này lại đúng?”, cũng như phác thảo một chứng minh thô sơ cho nhận định trên. Nói như Herbert Simon thì: “Solving a problem simply means representing it so as to make the solution transparent”.
Tuy nhiên, vấn đề cũng đến từ đây: Việc sử dụng một layer cuối khá đơn giản như logistic hay softmax, dẫn đến việc rất dễ thay đổi kết quả của mô hình, nếu như ta có thể chỉnh sửa được dữ liệu đầu vào. Tức là với các điểm dự đoán nằm gần decision boundary, ta sẽ có cách thay đổi dữ liệu đầu vào, sao cho về mặt ý nghĩa thì bản chất của dữ liệu không thay đổi, như trong hình chú gấu trúc, mà lại có thể làm “xê dịch” dự đoán mới sang một decision region khác, hoặc “cực đoan” hơn, như trong bài báo mới đây, chỉ cần thay đổi 1 pixel duy nhất.
Vậy tại sao ta không dùng một hàm số phức tạp/“có ý nghĩa” hơn cho lớp cuối của mô hình? Lý do các hàm logistic hay softmax được chọn là: Khi áp dụng các phương pháp tối ưu cho “mạng neuron”, với lượng dữ liệu lớn, một chiến thuật hay được sử dụng là huấn luyện theo từng “batch” nhỏ, và việc tính sai số đối với các hàm số kể trên nhìn chung là đơn giản. Như đề xuất của Colah, một ý tưởng tự nhiên là: Thay vì sử dụng các hàm số kể trên, ta có thể sử dụng thuật toán kNN ở lớp cuối cùng, với hai hướng như sau:
Sử dụng ở “test time”: Nghĩa là vẫn huấn luyện “mạng neuron” bằng layer cuối là các hàm logistic và softmax, sử dụng toàn bộ representation học được cho đến trước lớp cuối cùng rồi đưa ra dự đoán bằng kNN. Cách này nhìn chung có làm giảm sai số của mô hình thêm 0.1-0.2% ở một số bộ dữ liệu, nhưng vẫn không quá đáng kể.
Sử dụng trong lúc huấn luyện: Trong cách trên, mô hình “vẫn” tối ưu mạng sao cho các tập dữ liệu “tách biệt tuyến tính”. Việc “đòi hỏi” mô hình phải làm như vậy, theo Colah, là không hợp lý lắm. Điểm khó khăn của việc sử dụng thuật toán kNN cho lớp cuối cùng là: Tính lỗi như thế nào? Nếu mỗi “batch” huấn luyện phải dùng toàn bộ dữ liệu, thì chi phí tính toán lại quá cao. Colah có thử nhiều kiến trúc khác nhau, trong đó cố gắng vừa hạn chế được việc phải dùng hoàn toàn bộ dữ liệu cho mỗi “batch”, vừa đưa ra được một cách tính sai số khả dĩ cho từng “batch”, nhưng.. lại không có được kết quả tốt.
Trang 19: Nhìn chung, có các hướng regularization, là tên gọi chung cho các phương pháp giảm độ “overfitting” của mô hình, như sau:
Sử dụng mô hình đơn giản hơn. (Thanks Captain Obvious!)
Sử dụng L1 và L2 regularization: Đây là hai phương pháp được sử dụng rất nhiều trong cả Machine learning cổ điển lẫn Deep learning. Tinh thần của phương pháp này là sẽ “phạt” các hệ số có giá trị lớn, bởi giá trị lớn của các hệ số thường làm cho mô hình nhạy cảm hơn với những thay đổi nhỏ của dữ liệu đầu vào.
Sử dụng Dropouts: Đây được xem là một trong những phát kiến đã làm gã khổng lồ Deep learning tỉnh giấc, sau gần 20-30 năm “AI winter” (Geoffrey Hinton cùng các đồng sự viết bài báo về thuật toán “Lan truyền ngược”, Back-propagation, từ năm 1986, mà ý tưởng về thuật toán này đã manh nha từ những năm 1960s; mô hình Long Short-Term Memory (LSTM) của Jürgen Schmidhuber và các đồng nghiệp được đề xuất từ năm 1997; Yann LeCun cho ra đời mạng LeNet, với kiến trúc CNN, vào năm 1998), dĩ nhiên là đi cùng với sự phát triển về độ lớn của dữ liệu và phần cứng máy tính. Phương pháp này được lần đầu tiên ứng dụng vào mô hình AlexNet, là sự kết hợp của “hàm kích hoạt” ReLU và Dropouts, giúp một mô hình Deep learning giành chiến thắng tại một cuộc thi ImageNet sau khoảng một thập kỷ.
Phương pháp Dropouts có cách hoạt động như sau: Với từng “neuron” ở các lớp có Dropouts, sẽ có một xác xuất
$ p $cho việc “drop” đi “neuron” đó trong lần huấn luyện hiện tại, ie. đặt “trọng số” (weight) của “neuron” đó bằng 0, còn khi đưa ra dự đoán (“inference phrase”) thì sẽ sử dụng mạng được huấn luyện hoàn chỉnh (không có Dropouts).Ý nghĩa của phương pháp này là: Với mỗi đợt huấn luyện, mô hình được học sẽ “như” một “mạng neuron” “mới”, và mô hình cuối cùng sẽ tương đương với việc “ensemble” vô số “mạng neuron” khác nhau, với một niềm tin có cơ sở là chúng sẽ cho kết quả tốt hơn. Mặt khác, việc “làm khó” quá trình huấn luyện, bằng cách ngẫu nhiên đặt các hệ số bằng 0, cũng phần nào ép “mạng neuron” không dựa vào một nhóm nhỏ các “neuron” cụ thể nào, dẫn đến việc “mạng neuron” khái quát hoá tốt hơn, với các “neuron” mang lại nhiều thông tin hơn, lại tránh được các vấn đề kỹ thuật như exploding/vanishing gradients.
Trang 20: Ngoài các phương pháp như trên thì còn có một số kỹ thuật Regularization khác, liên quan đến việc chỉnh sửa dữ liệu đầu vào, đặc biệt là trong Computer Vision:
Data augmentation: Phương pháp này đơn giản là “sửa” dữ liệu đi một chút, như việc áp thêm nhiễu vào ảnh, được trình bày trong bài báo của Ian Goodfellow, đã nhắc đến bên trên. Điểm mấu chốt là làm sao “sửa” được dữ liệu, mà không thay đổi đi ý nghĩa của nó quá nhiều:
Như trong các bộ dữ liệu với “numerical features”, việc thu nhập một người có là $100k hay $100.1k, thì về bản chất, có lẽ cũng không khác nhau quá nhiều trong việc dự đoán xem người đó có trả được nợ hay không.
Với dữ liệu là định dạng ảnh thì ta có thể lấy đối xứng gương, xoay hình, hay tịnh tiến hình, mà không sợ làm mất đi ý nghĩa của dữ liệu.
Đây cũng là một trong số nhiều cách “làm giàu” thêm cho bộ dữ liệu một cách hiệu quả, do từ một điểm dữ liệu có thể sinh ra nhiều điểm dữ liệu khác có cùng nhãn. Ý tưởng của phương pháp này là tìm cách gây ra khó khăn cho mô hình khi huấn luyện, để thông tin được học không bị “overfitting” vào những “pattern” đơn giản nhưng không có giá trị phổ quát.
Test-time augmentation: Phương pháp này diễn ra trong quá trình dự đoán. Ý tưởng là sau khi có được một mô hình hoàn chỉnh, thì mỗi khi phải dự đoán 1 điểm dữ liệu, ta dùng phương pháp Data augmentation bên trên để sinh thêm
$ n $điểm dữ liệu khác. Mô hình lúc này sẽ đưa ra dự đoán cho$ n + 1 $điểm dữ liệu này, và “ensemble” các dự đoán đó thành một dự đoán cuối cùng.Bằng việc bắt mô hình phải đưa ra những dự đoán khác nhau rồi mới tổng hợp lại, phương pháp này sẽ hạn chế được những trường hợp như mô hình “overfitting” vào một pattern không có nhiều ý nghĩa và đưa ra dự đoán sai với “độ tin cập” cao, bằng cách ép mô hình phải đưa ra những dự đoán khác cho các điểm dữ liệu có cùng ý nghĩa. Trong Natural Language Processing, một kỹ thuật tương tự cũng được sử dụng trong các mô hình ngôn ngữ:
Phương pháp “Greedy”: Ở mỗi bước, một mô hình ngôn ngữ sẽ chọn một từ/cụm từ/ký tự mà nó cho là có khả năng xuất hiện nhất. Phương pháp này tương ứng với việc đưa ra dự đoán mà không có “Test time augmentation”.
Phương pháp “Beam search”: Thay vì chọn duy nhất một lựa chọn có khả năng xuất hiện nhất, ở mỗi bước, mô hình sẽ chọn
$ k $lựa chọn có khả năng xuất hiện nhất. Từ đó, mô hình phát phát triển thêm, nhưng vẫn đảm bảo ở mỗi bước chỉ có tối đa$ k $khả năng được xét đến. Cuối cùng, sau$ n $bước, mô hình chọn chuỗi có khả năng xuất hiện cao nhất trong số các chuỗi đã được xét đến. Xem chi tiết hơn tại đây.
“Test time augmentation” trong Computer Vision tương ứng với phương pháp “Beam search” với số bước là 1 (chỉ ensemble
$ k $lựa chọn có khả năng tốt nhất ở bước đầu tiên).
Trang 21 - 23: Lại trở về với cuộc thi của numer.ai.
Nói một chút về việc sử dụng Regularization trong mô hình Deep learning của mình ở cuộc thi của numer.ai. Các phương pháp như L1/L2 regularizations, Dropouts nhìn chung hoạt động tốt, trong khi những phương pháp đòi hỏi việc thêm “nhiễu” vào dữ liệu thì lại không hoạt động tốt. Điều này thật ra cũng.. dễ hiểu, bởi bản thân dữ liệu đã được áp thêm một lớp mã hoá, và do bản thân của dữ liệu được trích từ thị trường chứng khoán, vốn đã nhiều nhiễu hơn thông tin, thì việc thêm vào một lớp nhiễu nữa là hại nhiều hơn lợi.
Nghĩ lại về các phương pháp Regularization hiện tại thì thấy: Phần lớn các phương pháp augmentation trong Regularization thường tìm cách thêm “nhiễu” vào hoặc là dữ liệu đầu vào (như Data augmentation), hoặc thêm nhiễu vào dự đoán (như Test-time augmentation). Hay như trong Reinforcement learning, một phần quan trọng của thuật toán (Deep) Q-learning là thêm “nhiễu” vào hành động, tức lớp cuối cùng của mô hình.
Một ý tưởng tự nhiên đến là: Thêm nhiễu vào chính mô hình, thay vì các lớp đầu và cuối, mà cụ thể ở đây là trọng số của các “neuron” trong “mạng neuron”. Ý tưởng này đem đến cho mình một trong những mô hình tốt nhất khi dự cuộc thi của numer.ai, đó là sử dụng một mạng “shallow” với 2 lớp ẩn, và “thô thiển” thêm nhiễu dạng Gaussian vào các trọng số của neuron.
Trang 24 - 26:
[← Bấm vào đây] Có một chứng minh toán học khá đẹp đẽ cho sự hiệu quả của phương pháp này…
Thật ra là không có.
Khoảng một năm sau lúc mình sử dụng kỹ thuật đó trong cuộc thi của numer.ai thì OpenAI có công bố một bài báo chi tiết hơn về kỹ thuật này, với nhiều tìm kiếm rất thú vị!
Thay vì thêm “nhiễu” một cách “thô thiển” với biên độ bằng nhau ở các lớp, OpenAI đề xuất một phương pháp thêm “nhiễu” khá thú vị, mà cũng rất tự nhiên: Ở các lớp đầu tiên thì biên độ của “nhiễu” được thêm vào mạnh hơn, và biên độ “nhiễu” sẽ giảm dần theo độ sâu của mạng. Sự thay đổi về biên độ này xuất phát từ việc: Ở một “mạng neuron” đủ “sâu”, các lớp khác nhau sẽ có sự “nhạy cảm” khác nhau với cùng một biên độ “nhiễu”. Không chỉ thế, OpenAI cũng đề xuất một cơ chế phức tạp, để từ “sai số” của mô hình mà có thể tinh chỉnh “nhiễu” ở từng lớp sao cho “phù hợp”.
Video này có cho thấy sự khác biệt rõ rệt của việc sử dụng phương pháp này, đặc biệt là trong môi trường Walker2D:
“Agent” ban đầu chỉ cố gắng tiến về phía trước “bằng mọi giá”, mà không quan tâm đến “ý nghĩa” của hành động của mình, khi dùng phần “đầu” và “chi trước” để di chuyển về phía trước.
Còn khi được huấn luyện với phương pháp này, “agent” có hướng tiếp cận “hợp lý” hơn, cụ thể là bằng việc di chuyển bằng cả hai “chi” mà không sử dụng phần “đầu”, và hiệu quả hơn. “Agent” cũng học được cách “búng chân”, để có thể di chuyển nhanh hơn về phía trước.
Trang 27 - 29:
Dĩ nhiên là OpenAI cũng không chứng minh được, một cách chặt chẽ về mặt toán học, vì sao phương pháp này lại hiệu quả hơn. Nói một cách vĩ mô thì “landscape” hiện tại của Deep learning không được xây dựng vững chãi bằng các lý thuyết toán học đồ sộ. Ta không chắc rằng một mô hình Deep learning mà ta đang huấn luyện sẽ cho kết quả “tối ưu” (global optima), “đủ tốt”, hay có “sai số” bao nhiêu với các kết quả “tối ưu”/“đủ tốt”.
Cuối cùng thì, như George Box nói: “Essentially, all models are wrong, but some are useful”. Deep learning hiện tại thật ra gần với một ngành kỹ thuật, hay khoa học thực nghiệm, hơn là khoa học chính xác.
Nhưng đó cũng là thứ làm cho công việc của những người làm Deep learning “thi vị” hơn. Ta đang ở “phía bên này” của lịch sử, đang ở “the new Age of Discovery”, nơi mà chỉ một phát kiến mới, một lý thuyết toán học chặt chẽ, có thể thay đổi toàn bộ lịch sử của ngành Deep learning, mà nói xa hơn là Trí tuệ nhân tạo, và cho nó một diện mạo hoàn toàn mới. Cái phát kiến ấy có thể không bao giờ đến, có thể 100 năm nữa mới đến, mà cũng có thể lúc này đây đang nằm trên một trang nháp, hay trong vài dòng code còn dang dở trên một Jupyter Notebook ở một viện nghiên cứu nào đó.
What a time to be alive!
Cảm ơn mọi người đã lắng nghe.